PERTEMUAN 09 ATURAN SUBSTITUSI INTEGRAL TAK TENTU FUNGSI EKSPONENSIAL

pada tanggal

ATURAN SUBSITUSI INTEGRAL TAK TENTU FUNGSI EKSPONENSIAL

Integral Eksponensial

    Fungsi eksponensial biasanya dinotasikan dengan ex. Beberapa konsep dasar yang harus dipelajari dalam integral eksponensial yaitu

Rumus Integral Exponensial
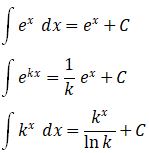
Integral Eksponensial

Keterangan:

  • ex, ekx : fungsi eksponensial
  • C     : konstanta

Integral Tak Tentu Fungsi Eksponensial 

    Untuk mengetahui integral fungsi eksponensial perlu diketahui terlebih dahulu turunan dari fungsi eksponensial berikut.

    Dari turunan tersebut dapat disimpulkan bahwa integral fungsi eksponensial dapat ditulis:

    Pengembangan dari rumus di atas adalah dengan menggunakan aturan substitusi dengan bentuk dasar sebagai berikut.

Langkah-langkah Menyelesaikan Integral Tak Tentu Fungsi Eksponensial 

    Dengan Aturan Substitusi Untuk memudahkan penyelesaian persoalan integral tak tentu fungsi eksponensial dengan aturan substitusi, perlu diperhatikan langkah-langkah berikut. 

a. Pastikan fungsi integran berbentuk dasar ∫[g(x)] rg ′ (x)dx. Jika belum, ubahlah menjadi bentuk tersebut 

b. Misalkan pangkat dari fungsi eksponensial menjadi fungsi u 

c. Turunkan fungsi u sehingga diperoleh du = .... dx 

d. Nyatakan nilai dari dx agar sesuai dengan soal yang diberikan, kemudian substitusikan pemisalan tadi ke integral semula


Soal yang ada di modul : 




Komentar

Posting Komentar