Integral Trigonometri
Sebelum memahami integral tak tentu fungsi trigonometri, terlebih dulu harus diketahui bahwa trigonometri berasal dari kata Yunani, yaitu trigonon : tiga sudut, dan metron : mengukur. Sehingga secara istilah, trigonometri diartikan sebagai sebuah cabang matematika yang mempelajari hubungan yang meliputi panjang dan tiga sudut segitiga siku-siku. Dari definisi tersebut, maka dapat dijelaskan bahwa fungsi trigonometri merupakan fungsi yang didalamnya terdapat hubungan panjang dan tiga sudut segitiga siku-siku. Fungsi dasar trigonometri dikelompokkan menjadi 6 jenis, yaitu:
a. sin 𝑥
b. cos 𝑥
c. tan 𝑥 = sin𝑥 cos 𝑥
d. sec 𝑥 = 1 cos 𝑥
e. cosec 𝑥 = 1 sin 𝑥
f. cot 𝑥 = cos 𝑥 sin 𝑥
Sudut-Sudut Pada Fungsi Trigonometri
dibagi menjadi 4 kuadran, yaitu:
a. Kuadran I
Daerah kuadaran I meliputi daerah yang dibatasi sudut 0º ≤ x ≤ 90º . Pada kuadran ini sin x dan cos x bernilai positif, sehingga mengakibatkan tan x, sec x, cosec, dan cot x juga bernilai positif. Kuadran I berlaku sifat-sifat berikut.
1) sin (90º + x) = cos x
2) cos (90º + x) = sin x
3) tan (90º + x) = cot x
4) sec (90º + x) = cosec x
5) cosec (90º + x) = sec x
6) cot (90º + x) = tan x
b. Kuadran II
Daerah kuadaran II meliputi daerah yang dibatasi sudut 90º ≤ x ≤ 180º . Pada kuadran ini sin x bernilai positif, sedangkan cos x bernilai negatif, sehingga mengakibatkan cosec x bernilai positif, tetapi tan x, sec x, dan cot x juga bernilai negatif. Kuadran II berlaku sifat-sifat berikut.
1) sin (90º + x) = cos x
2) cos (90º + x) = -sin x
3) tan (90º + x) = -cot x
4) sec (90º + x) = -cosec x
5) cosec (90º + x) = sec x
6) cot (90º + x) = - tan x
7) sin (180º - x) = sin x
8) cos (180º - x) = -cos x
9) tan (180º - x) = -tan x
10) sec (180º - x) = -sec x
11) cosec (180º - x) = cosec x
12) cot (180º - x) = -cot x
c. Kuadran III
Daerah kuadaran III meliputi daerah yang dibatasi sudut 180º ≤ x ≤ 270º. Pada kuadran ini sin x dan cos x bernilai negatif, sehingga mengakibatkan cosec x dan sec x bernilai negatif, sedangkan tan x dan cot x bernilai positif. Kuadran III berlaku sifat-sifat berikut.
1) sin (180º + x) = -sin x
2) cos (180º + x) = -cos x
3) tan (180º + x) = tan x
4) sec (180º + x) = -sec x
5) cosec (180º + x) = -cosec x
6) cot (180º + x) = cot x
7) sin (270º - x) = -cos x
8) cos (270º - x) = -sin x
9) tan (270º - x) = cot x
10) sec (270º - x) = -cosec x
11) cosec (270º - x) = -sec x
12) cot (270º - x) = tan x
d. Kuadran IV
Daerah kuadaran IV meliputi daerah yang dibatasi sudut 270º ≤ x ≤ 360º . Pada kuadran ini sin x bernilai negatif, sedangkan cos x bernilai positif, sehingga mengakibatkan sec x bernilai positif, sedangkan cosec x, tan x, dan cot x bernilai negatif. Kuadran III berlaku sifat-sifat berikut.
1) sin (270º + x) = -cos x
2) cos (270º + x) = sin x
3) tan (270º + x) = -cot x
4) sec (270º + x) = cosec x
5) cosec (270º + x) = -sec x
6) cot (270º + x) = -tan x
7) sin (360º - x) = -sin x
8) cos (360º - x) = cos x
9) tan (360º - x) = -tan x
10) sec (360º - x) = sec x
11) cosec (360º - x) = -cosec x
12) cot (360º - x) = -cot x
Integral Tak Tentu Fungsi Trigonometri
Integral tak tentu fungsi trigonometri merupakan “bentuk integral yang integralnya berbentuk fungsi trigonometri dan memiliki variabel integrasi yang tak terbatas”. Karena variabel integrasinya tidak memiliki batasan, maka hasil dari integral tak tentu fungsi trigonometri hanyalah berupa penyelesaian umum yang juga dalam bentuk fungsi trigonometri ditambah dengan tetapan integrasi yang disimbolkan dengan huruf c. Karena fungsi integran (fungsi yang diintegralkan) berbentuk fungsi trigonometri, maka penyelesaiannyapun melibatkan beberapa konsep atau identitas trigonometri.
Rumus Dasar Fungsi Trigonometri
Seperti yang sudah dibahas pada bab sebelumnya, bahwa integral adalah operasi balikan dari turunan, maka fungsi trigonometri dapat diselesaikan dengan berpatokan pada hasil dari turunan beberapa fungsi trigonometri. Untuk mempermudah pemahaman tentang rumus dasar fungsi trigonometri, perhatikan tabel di bawah ini :
| No. | Fungsi f(x) = y | Turunan  | Integral |
| 1 | y = sin x | cos x | 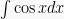 = sin x = sin x |
| 2 | y = cos x | – sin x | 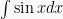 = – cos x = – cos x |
| 3 | y = tan x | sec2 x |  = tan x = tan x |
| 4 | y = cot x | – csc2 x |  = – cot x = – cot x |
| 5 | y = sec x | tan x . sec x |  = sec x = sec x |
| 6 | y = csc x | -.cot x . csc x |  = – csc x = – csc x |
Selain rumus dasar diatas, ada rumus lain yang bisa digunakan pada pengoperasian integral trigonometri yaitu:
| Fungsi f(x) = y | Turunan  | Integral |
 | cos (ax + b) |  = =  sin (ax + b) + C sin (ax + b) + C |
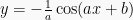 | sin (ax + b) | 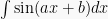 = = 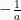 cos (ax + b) + C cos (ax + b) + C |
y =  tan (ax + b) tan (ax + b) | sec2 (ax + b) |  = =  tan (ax + b) + C tan (ax + b) + C |
y = 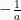 cot (ax + b) cot (ax + b) | csc2 (ax + b) | 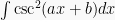 = = 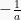 cot (ax + b) cot (ax + b) |
y = 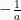 sec (ax + b) sec (ax + b) | tan (ax + b) . sec (ax + b) | 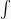 (ax+b) . sec(ax + b) dx= (ax+b) . sec(ax + b) dx=  sec (ax + b) + C sec (ax + b) + C |
y = 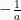 csc (ax + b) csc (ax + b) | cot (ax + b) . csc (ax + b) | 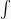 cot (ax + b) . csc (ax + b) dx = cot (ax + b) . csc (ax + b) dx = 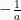 csc (ax + b) csc (ax + b) |
Aturan Kelinieran Integral Tak Tentu Fungsi
Trigonometri Sama seperti pada integral tak tentu fungsi aljabar, pada integral tak tentu fungsi trigonometri juga berlaku aturan kelinieran. Misalkan diketahui dua fungsi, yaitu fungsi f dan g, dimana kedua fungsi tersebut mempunyai integral, maka berdasarkan aturan kelinearan berlaku sifat sebagai berikut.
a. ∫ 𝑘 𝑓(𝑥) 𝑑𝑥 = 𝑘 ∫ 𝑓(𝑥)𝑑𝑥, 𝑘 = 𝑘𝑜𝑒𝑓𝑖𝑠𝑖𝑒𝑛
b. ∫[𝑓(𝑥) + 𝑔(𝑥)]𝑑𝑥 = ∫ 𝑓(𝑥)𝑑𝑥 + ∫ 𝑔(𝑥)𝑑𝑥
c. ∫[𝑓(𝑥) − 𝑔(𝑥)]𝑑𝑥 = ∫ 𝑓(𝑥)𝑑𝑥 − ∫ 𝑔(𝑥)𝑑x


Komentar
Posting Komentar